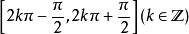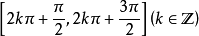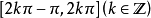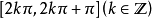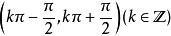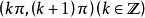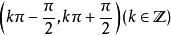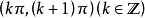三角函数求导公式

(sinx)' = cosx

(cosx)' = - sinx

(tanx)'=1/(cosx)^2=(secx)^2=1+(tanx)^2

-(cotx)'=1/(sinx)^2=(cscx)^2=1+(cotx)^2

(secx)'=tanx·secx

(cscx)'=-cotx·cscx

(arcsinx)'=1/(1-x^2)^1/2

(arccosx)'=-1/(1-x^2)^1/2

(arctanx)'=1/(1+x^2)

(arccotx)'=-1/(1+x^2)

(arcsecx)'=1/(|x|(x^2-1)^1/2)

(arccscx)'=-1/(|x|(x^2-1)^1/2)

(sinhx)'=coshx

(coshx)'=sinhx

(tanhx)'=1/(coshx)^2=(sechx)^2

(coth)'=-1/(sinhx)^2=-(cschx)^2

(sechx)'=-tanhx·sechx

(cschx)'=-cothx·cschx

扩展资料：

变化规律

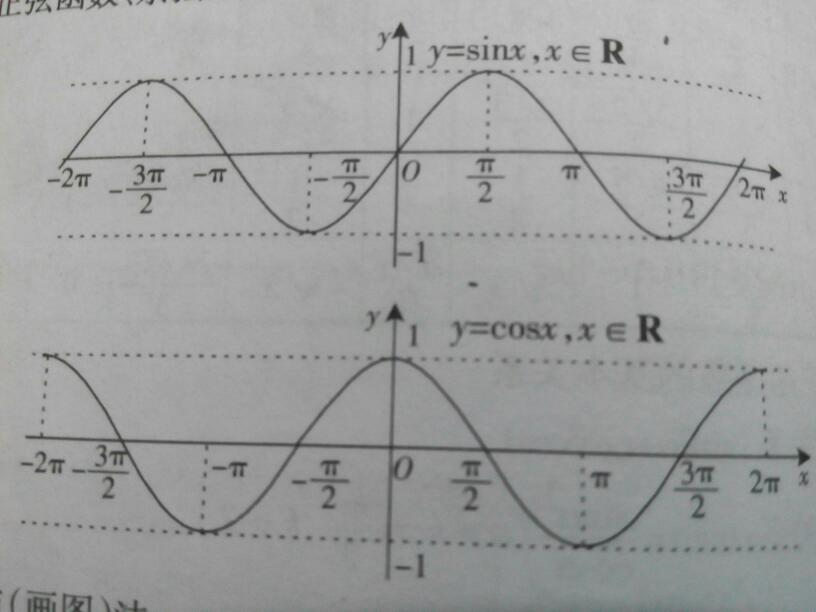
正弦值在

随角度增大（减小）而增大（减小），在

随角度增大（减小）而减小（增大）；

余弦值衡凯在

随角度增大（减小）而增大（减小），在

随角度增大（减小）而减小（增大）；

正切值在

随角蠢樱度增大（减小）而增大（减小）；

余切值在

随角度增大（减小）而减小（增大）；

正割值在

随着角度的增大（或减小）而增大（或减小）；

余割值在

随着角度的增大（或减小）而减小（或增大）。

参考资带拦丛料来源：百度百科—三角函数

标签：求导,三角函数,公式