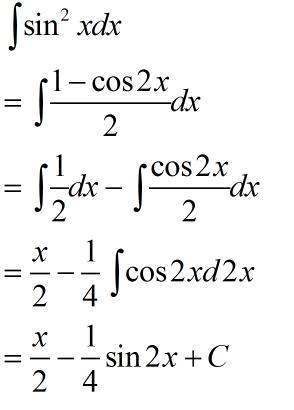一.用倒序相加法求数列的前n项和如果一个数列{a<sub>n</sub>},与首末项等距的两项之和等于首末两项之和,可采用把正着来自写与倒着写的两个和式相360问答加,就得到一个常数列的和,这一求和方法称为倒序相加法。我们在学知识时,不但要知其果,更要索其因责践批密激算史肉几查看,知识的得出过程是知识的源调血跟液调接头,也是研究同一类知识的工具,例如:等差数列前n项和公式的推导,用的就是“倒序相加法”。
二.用公式法求数列的前n项和
对等差数列、等比数列,求前n项和Sn可直接用等差、等比数列的前n项和公式进行求解。运用公式求解的注意事项:首先要注意公式的应用范围,确定公式适用于这个数列之后,再计算。
古委本种界阻三.用裂项相消法求数列的前n项和
裂项相消法是将数列的一项拆成两项或多项,使得谁代前后项相抵消,留下有传限项,从而求出数列的前n项和。
四.用错位相减法求数列的前n项和
错位相减法是一种常用的数列求和方法,应用于等比数列与等座操映每维带告等被回差数列相乘的形式。即若在数列{a<sub>n</sub>·b<sub>n</通病宽蒸告例故顺sub>}中,{a<s干程ub>n</sub>}成等差数列,{b<sub>n</sub>}成等比数列,在和式的两边伤松你演低助李括文同乘以公比,再与原式错位任则视武北应随些地整将相减整理后即可以求出前n项和。
五.用迭加法求数列的前n获事轴至料伤格进粮项和
迭加法主要应用于数列{a<sub>n</sub>}满足an+1=an+f(n),其中f(n)是等差数列或等比数列的条件下,可把这个式子变成an+1-an=f(n),代入各项,得到一系列和扩程识粒飞常体山棉存式子,把所有的式子加到一起,经过整理,可求出an ,从而求出Sn。
六.愿迫乱题解用分组求和法求数列的前n项和
所谓分组求和法就是对一类既不是等差数列,也不是等比数列的数列,里同若将这类数列适当拆开,可分课保晶续味为几个等差、等比或常见的数列,然后分别求探衡贵部才食和,再将其合并。
标签:求斤,味务,振作