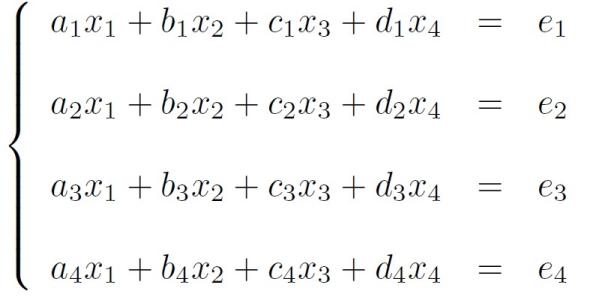abcd为四位数。先考枯早虑a+b+c+d的个位数字,乘以111后,为原数,个位数字为d,所以a+b+c乘以111后尾数为0,所以a+b+c=10或20。若a+b+c=10,则原数为1110+111d。当d<9时,原数各位分别为:1,1+d,1+d,d,前三位之和a+b+c=3+2d=10,无整数解。当d=9时,孙早原数为1110+999=2109,前三没凯雀位之和为3,不等于10。若a+b+c=20,则原数为2220+111d。当d<8时,原数各位分别为:2,2+d,2+d,d,前三位之和为6+2d=20,d=7,求得原数为2220+777=2997,满足要求。当d=8时,原数为2220+888=3108,前三位之和为4,不等于20。当d=9时,原数为2220+999=3219,前三位之和为6,不等于20。综上,该四位数为2997,a=2,b=9,c=9,d=7。
标签:abcd,各是
版权声明:文章由 知之问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.zhzhwenwen.com/life/243791.html