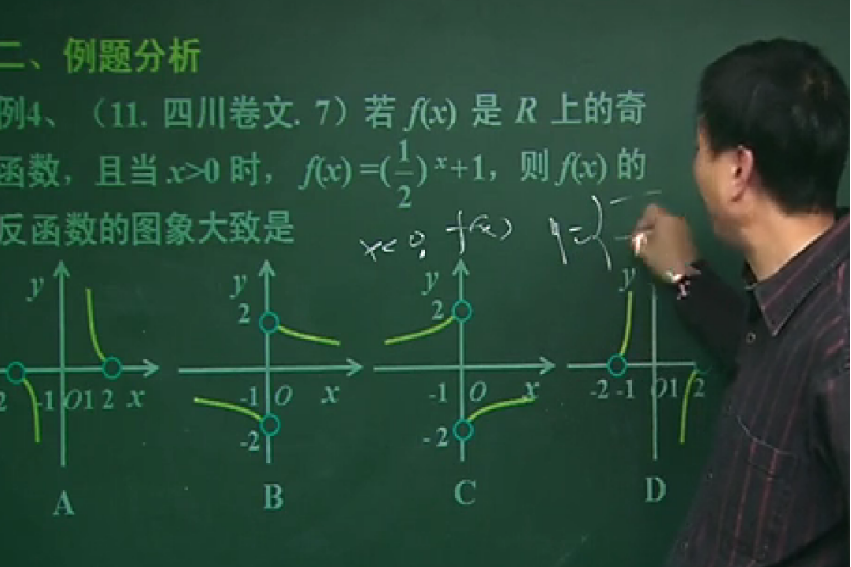什么是反函数

反函数就是将原函数中自变量与变量调换位置，用原函数的变量表示自变量而形成的函数。

一、反函数的符号。

反函数的符号记为f-1（x），在中国桐凳的教材里，反三角函数记为arcsin、arccos等等，但是在欧美一些国家，sinx的反函数记为sin-1（x）。

二、反函数的性质。

1、函数存在反函数的充要条件是，函数的定义域与值域是一一映射。

2、一个函数与它的反函数在相应区间上单调性一致磨轮戚。

3、大部分偶函数不存在反函数（当函数y=f（x），定义域是{0}且f（x）=C（其中C是常数），则函数f（x）是偶函数且有反函数，其反函数的定义域是{C}，值域为{0}）。奇函数不一定存在反函数，被与y轴垂直的直线截时能过2个及以上点即没有反函数。

4、若一个奇函数存在反函数，则它的反函数也是奇函数。

5、一段连续的函数的单调性在对应区间内具有一致性。

6、严增（减）的函数一定有严格增（减）的反函数。

7、反函数是相互的且具有唯一性。

8、定义域、值域相反对应法则互逆（三反）。

反函数的应用：

1、温度转换。

摄氏度和华氏度之间的转换就是一个反函数的例子。如果知道一个温度的摄氏度，可以通过反函数计算出对应的华氏度。

2、货币兑换。

不同国家的货币之间的兑换也是一个反函数的例子如果知道一个货币的汇率，可以通过反函数计算出对应的另一种货币的汇率。

3、身高体重指数。

身高体重指数（BMI）是一个反函数的例子。如果知道一个人的身高和体重，可以通过反函数计算出对应的BMI值。

4、电阻电流电压。

电阻、电流和电压之间的关系也是一个反函数的例子。如果知道瞎陵一个电阻的值和电流的大小，可以通过反函数计算出对应的电压大小。

标签：反函数