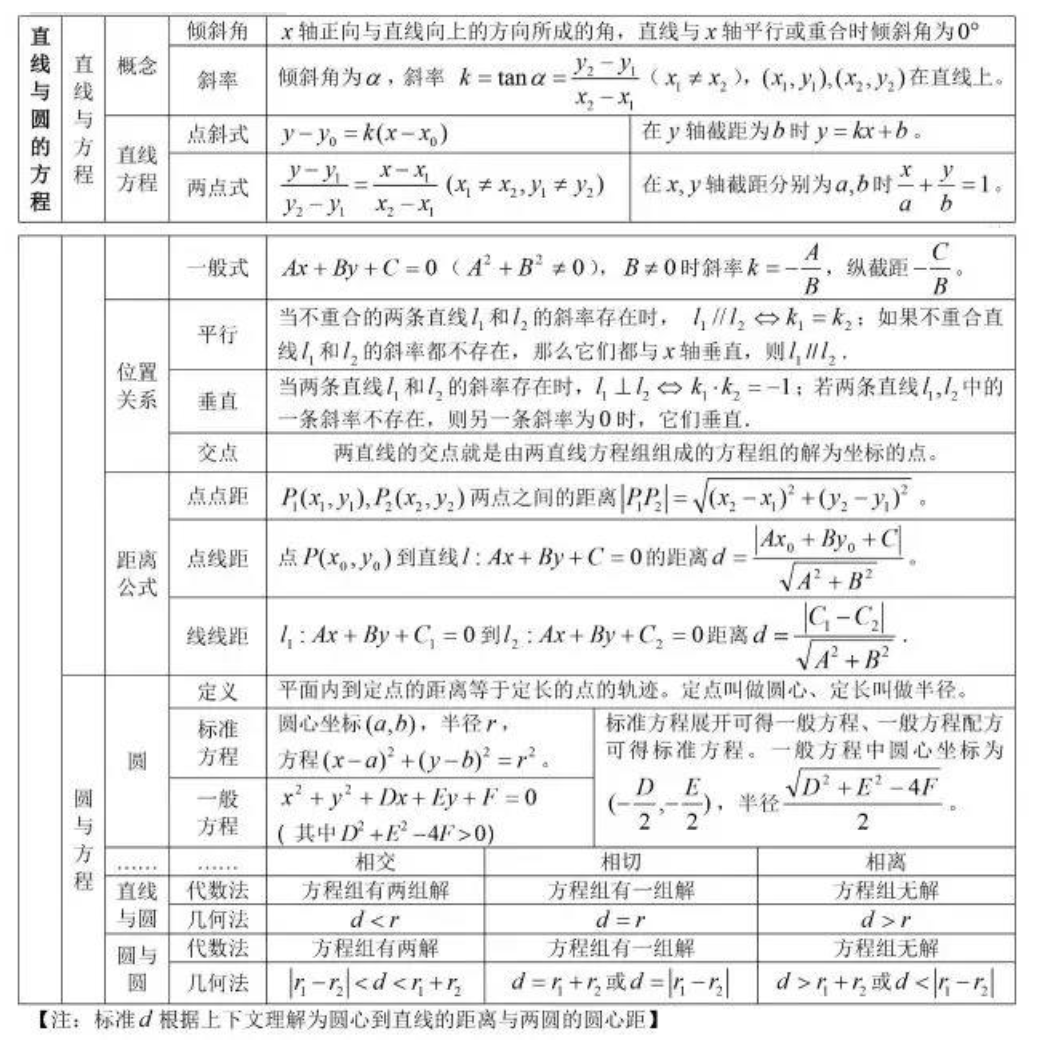
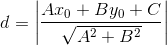公式中方程为Ax+By+C=0,点P的坐标为(x0,y0)。
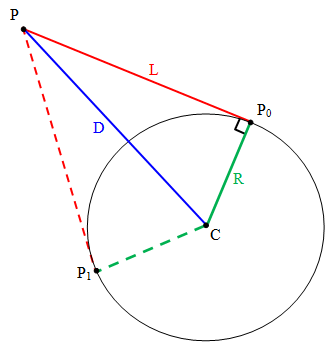
假设点坐标为(dx,dy), 曲线方程为f(x,y)=0, 从隐曲线最近点(u,v)到该点的向量必垂直于曲线,因此可以通过寻找满足下式的点获得最近点:
1)(u,v)指手是曲线上的一点,满足f(u,v)=0;
2)向渗做量s=(dx,dy)-(u,v), 即 (dx-u, dy-v);
求出所有的s,其中最短的丛逗衡距离即为点到曲线的距离。
扩展资料:
根据定义,点P(x₀,y₀)到直线l:Ax+By+C=0的距离是点P到直线l的垂线段的长,
设点P到直线的垂线为l',垂足为Q,则l'的斜率为B/A
则l'的解析式为y-y₀=(B/A)(x-x₀)
把l和l'联立得l与l'的交点Q的坐标为((B^2x₀-ABy₀-AC)/(A^2+B^2), (A^2y₀-ABx₀-BC)/(A^2+B^2))
由两点间距离公式得
PQ^2=[(B^2x₀-ABy₀-AC)/(A^2+B^2)-x0]^2
+[(A^2y₀-ABx₀-BC)/(A^2+B^2)-y0]^2
=[(-A^2x₀-ABy₀-AC)/(A^2+B^2)]^2
+[(-ABx₀-B^2y₀-BC)/(A^2+B^2)]^2
=[A(-By₀-C-Ax₀)/(A^2+B^2)]^2
+[B(-Ax₀-C-By₀)/(A^2+B^2)]^2
=A^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
+B^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(A^2+B^2)(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(Ax₀+By₀+C)^2/(A^2+B^2)
所以PQ=|Ax₀+By₀+C|/√(A^2+B^2),公式得证。
参考资料:百度百科——点到直线距离
标签:点到,直线,公式