正弦型函数

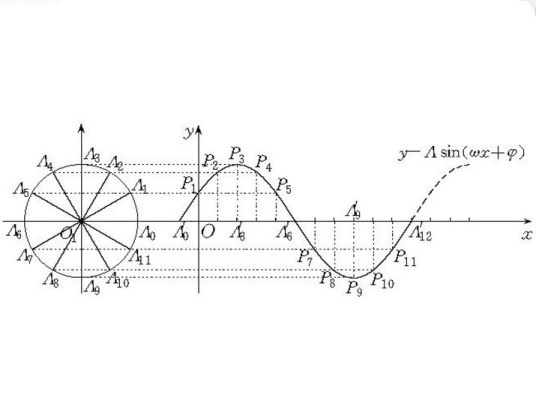
正弦型函数是形如y=Asin(ωx+φ)+k的函数，其中A，ω，φ，k是常数，且ω≠0。函数y=Asin(ωx+φ)，(A>0，ω>0)，x∈R的图象可以看作是用下面的方法得到的：先把y=sinx的图象上所有的点向左(φ>0)或向右(φ<0)平行移动|φ|个单位，再把所得各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的1/ω倍(纵坐标不变)，再把所得各点的纵坐标伸长(A> 1)或缩短(0 0，ω> 0)，x∈〔0，+∞)表示一个振动量时，A就表示这个量振动时离开平衡位置的最大距离，通常把它叫做振动的振幅；往复振动一次所需要的时间T=2π/ω，它叫做振动的周期。单位时间内往复振动的次数f=1/T=ω/2π，它叫做振动的频率，ωx+φ叫做相位，φ叫做初相(即当x=0时的相位 )。

想要了解更多“正弦型函数”的信息，请点击：正弦型函数百科

标签：正弦型函数,型函数,正弦,图像