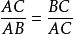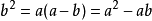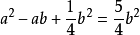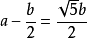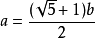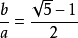黄金分割0.618是怎么计算出来的

黄金分割是将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值。

计算方法如下：设一条线段AB的长度为a，C点在靠近B点的黄金分割点上，且AC为b，则a比b就是黄金数；

（√5-1）：2，近似值为0.618，通常用希腊字母Ф表示这个值。这个比例被公认为是最能引起美感的比例，因此被称为黄金分割。

扩展资料：

黄金孙改分割的起源：现在人一般认为，黄金分割是由公元前6世纪的毕达哥拉斯发现的。系统论述黄金分割的最早记载是欧几里得的《几何原本》，在该书第四卷中记述了用黄金分割作五边形、十边形的的问题，则歼判在第二卷第11节中详细讲了黄金分割的计算方法，并称

0.618叫做“黄金数”。

在《几何原本》中把它称为“中末比”。直到文艺复兴时期，人们重新发现了古希腊数学，并且发现这种比例广泛存在于许多图形的自然结构之中，因而高度推崇中末比的奇妙性质和用途。

最早在著作中使用“黄金分割”这一名称的是德国数学家M·欧姆，他是发现电学的欧姆定律的G·S·欧姆的弟弟。改颂他在自己的著作《纯粹初等数学》（第二版，1835）中用了德文字：“der

goldene schnitt（黄金分割）”来表述中末比，以后，这一称呼才逐渐流行起来。

参考资料来源：百度百科-黄金分割

标签：黄金分割,计算出来