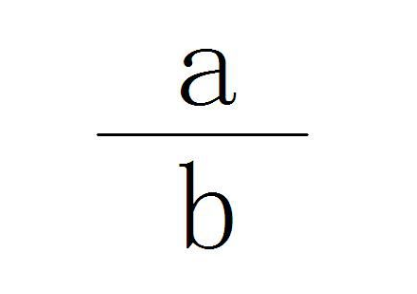意义:
我们在数物体的时候,用来表示物体个数的数1、2、3、4、5、……,叫做自然数,也叫做正整数。自然数的个数是无限的。
在自然数的前面加上“-”号,得到的数-1,-2,-3,-4,-5,……叫做负整数。负整数的个数也是无限的。
0既不是负整数也不是正整数。它可以用来表示一个物体也没有。
我们把正整数,0,负整数,统称为整数。
整数的全体构成整数集,整数集是一个数环。在整数系中,零和正整数统称为自然数。-1、-2、-3、…、-n、…(n为非零自然数)为负整数。则正整数、零与负整数构成整数系。整数不包括小数、分数。
如果不加特殊说明,我们所涉及的数都是整数,所采用的字母也表示整数。
我们以0为界限,将整数分为三大类:
1. 正整数,即大于0的整数如,1,2,3······直到。
2. 零,既不是正整数,也不是负整数,它是介于正整数和负整数的数。
3.负整数,即小于0的整数如,-1,-2,-3······直到。(n为正整数)
注:零和正整数统称自然数。
整数也可分为奇数和偶数两类。
整数中,能够被2整除的数,叫做偶数。不能被2整除的数则叫做奇数。即当n是整数时,偶数可表示为2n(n为整数);奇数则可表示为2n+1(或2n-1)。
偶数包括正偶数(亦称双数)、负偶数和0。所有整数不是奇数,就是偶数。
在十进制里,我们可用看个位数的方式判断该数是奇数还是偶数:个位为1,3,5,7,9的数为奇数;个位为0,2,4,6,8的数为偶数。
利用皮亚诺公理可以对正整数及N*进行如下描述:
任何一个满足下列条件的非空集合叫做正整数集合,记作N*。如果
Ⅰ 1是正整数;
Ⅱ 每一个确定的正整数a,都有一个确定的后继数a ,a也是正整数(数a的后继数a‘就是紧接在这个数后面的整数(a+1)。例如,1‘2,2’3等等。);
Ⅲ 如果b、c都是正整数a的后继数,那么bc;
Ⅳ 1不是任何正整数的后继数;
Ⅴ 设SN*,且满足2个条件(i)1∈S;(ii)如果n∈S,那么n∈S。那么S是全体正整数的集合,即SN*。(这条公理也叫归纳公理,保证了数学归纳法的正确性)
皮亚诺公理对N*进行了刻画和约定,由它们可以推出关于正整数的各种性质。
标签:整数,意义