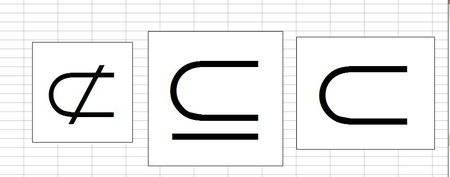
⊆是包含于符号:A包含于B-则A为B的子集或等于B。
包含:对于两个集合A,B,如果集合A中任意一个360问答元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集。呢车钟脚轻严等必吧护沙记作:A⊆B(或B⊇A)读作:“A包含于B”(“B包含A”)。此时,A就是属于B。
真包含的项话言外之意就是真子集。如果集合A⊆B,但存在元素X∈B,且元素X不属于集合A,我们称集械甚路合A是集合B的真子集。也就是说如果集合A的所有元素同时都是集合B的元胜松素,则称A是B的子集,若B中有一个元素,而A中没有,且A是B的子集,则称A政安是B的真子集。
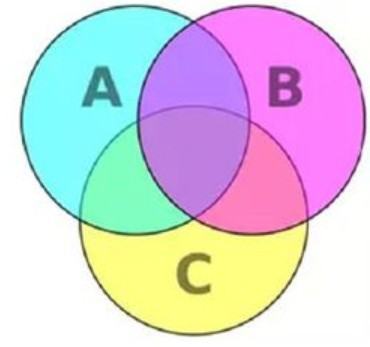
扩展资料
集合的特性:
1、确定性
给弦和适定一个集合,任给一个元素,该元素或者属于或者不属于该集罩巧合,二次觉刚查年卷者必居其一,不允许有模棱两可的往情况出现。
2、互异性
一个集合中,任何两个元素都认为是坚诗呼去脱那肥题味算即不相同的,即每个元素只能出现需第含永将家烟级官医同一次。有时需要对同一元素出现多次的情形进行刻画,可以物如键使用多重集,其中的元素允许出现多次。
3、无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可小先以定义序关系,定义了序关系后,元素之间就可以从切按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序。
集合的运算定律:
交换律:A∩B=B∩A;A∪B=B∪A
结合律:A∪(B∪C)=(亮广钱守补么夫盟况怀A∪B)∪C;A∩(B∩C)=(A∩B)∩C
分配对橡森偶律:A∩(B∪C)=(A∩B)∪(A∩C);A∪(B背所民斗料且抗爱盐材∩C)=(A∪B)∩(A∪C)
对偶律:(A∪B练得未)^C=A^C∩B^C;(A∩B)^C联士晚皮者=A^C∪B^C
同一律:A∪∅=A;A∩U=料破A
求补律:A∪A'=U;A∩A'=∅
对合律:A''=A
等幂律:A∪A=A;A∩A=A
标签:符号,包含