鸡兔同笼万能口诀

鸡兔同笼万能口诀如下：

鸡兔同笼巧记口诀是假设全是鸡，假设全是兔。多了几只脚，少了几只足?除以脚的差，便是鸡兔数。

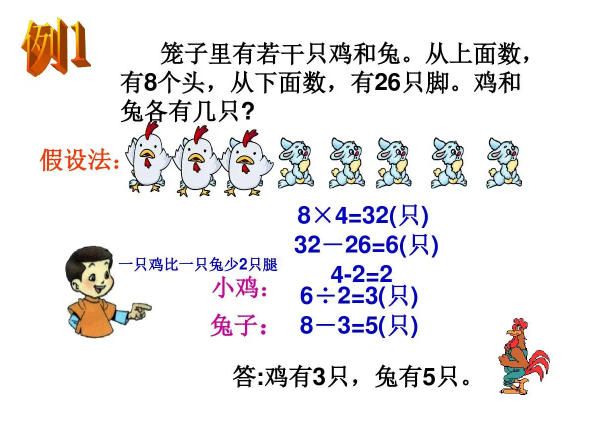
鸡兔同笼，是中国古代著名典型趣题之一，记载于《孙子算经》之中。鸡兔同笼问题，是小学奥数的常见题型。在它的解法中，通常是假设法比较简单易懂一点。

鸡兔同笼的问题是小学五年级的数学问题，这不光是一种数学问题，更是一种数学的思想。

分析解戚雀法销仔档

题目为鸡兔同笼，有头36，有脚120，求鸡兔数。

假设全是鸡，假设全是兔。

我们拿到题目后，可以将笼中的鸡兔同笼先假设为笼中全部是鸡，或者全部是兔子。如果假设全是鸡，那么笼子里这36个头就都是鸡的头，那么就是有36只鸡，而我们都知道鸡都是两条腿的，那鸡的腿总数应该是个数的两倍，也就是36×2=72只

多了几只脚，少了几只足?

和其他条件再去比对下，看差距是多少。和题目中的另一个已知条件，脚有120只去比对，会发现脚少了120-72=48条腿，因为每只鸡的腿比兔子少2个，也亏乱就是说这少的都是兔子的腿。

除以脚的差，便是鸡兔数。

将假设条件下的腿之间相差的数量除以2，就是鸡和兔子的数量。在上面的假设中，我们得到的结果是和已知条件中腿的数量相差48条腿，那除以2就是24，也就是说兔子的个数是24只。

在以后的数学学习中，经常会用到假设条件，就像这道鸡兔同笼的题目，通过假设，可以变形出很多条件。这个口诀提到的方法，还是相对简单易懂的，其实不仅可以假设笼中都是鸡或者兔子。

标签：鸡兔同笼,口诀,万能